Dans cette section, nous allons étudier la limite de ln(x) / x en mathématiques, et comprendre son importance dans l’analyse mathématique.
La fonction ln(x) / x est l’un des concepts clés en mathématiques. Elle permet d’étudier le comportement d’une fonction logarithmique naturelle divisée par la variable x lorsque x tend vers l’infini ou zéro.
Comprendre cette limite est essentiel pour l’analyse mathématique, car elle joue un rôle crucial dans divers domaines tels que la théorie des nombres, la géométrie différentielle et l’analyse fonctionnelle.
Dans les sections suivantes, nous allons explorer en détail la fonction ln(x) / x, comprendre comment calculer sa limite, étudier son comportement et découvrir ses différentes applications en mathématiques.
Les points clés à retenir :
- La limite de ln(x) / x est importante pour l’analyse mathématique.
- Cette limite permet d’étudier le comportement de fonctions logarithmiques.
- Elle est utile dans de nombreux domaines mathématiques.
- La limite peut être calculée en suivant des étapes spécifiques.
- La fonction ln(x) / x présente des caractéristiques intéressantes.
Maintenant que nous avons établi le contexte, passons à une brève présentation de la fonction ln(x) dans la section suivante.
Présentation de la fonction ln(x)
La fonction ln(x), également connue sous le nom de logarithme népérien, est une fonction logarithmique très importante en mathématiques. Elle permet de calculer le logarithme d’un nombre en utilisant la base e, où e est une constante mathématique d’environ 2,71828.
Le logarithme népérien est couramment utilisé dans de nombreux domaines des mathématiques, tels que l’analyse, la théorie des probabilités, la géométrie différentielle, et bien d’autres. Il est souvent noté comme ln(x), où x est le nombre dont nous souhaitons calculer le logarithme.
La fonction ln(x) a de nombreuses propriétés intéressantes et est largement utilisée pour résoudre des équations exponentielles et des problèmes impliquant la croissance et la décroissance exponentielles.
Propriétés de la fonction ln(x)
Voici quelques propriétés importantes de la fonction ln(x) :
- ln(x) est défini uniquement pour les nombres réels strictement positifs.
- ln(1) = 0, car le logarithme népérien de 1 est toujours égal à zéro.
- ln(e) = 1, puisque le logarithme népérien de la constante e est égal à un.
- ln(x * y) = ln(x) + ln(y), ce qui signifie que le logarithme du produit de deux nombres est égal à la somme des logarithmes des deux nombres individuels.
Il est également important de noter que la fonction ln(x) est strictement croissante, ce qui signifie que si x1
Pour une meilleure compréhension de la fonction ln(x), voici un tableau illustrant quelques exemples de calculs de logarithmes népériens :
| x | ln(x) |
|---|---|
| 1 | 0 |
| 2 | 0.6931 |
| 3 | 1.0986 |
| 4 | 1.3863 |
Comme le tableau le montre, le logarithme népérien d’un nombre x augmente généralement lorsque x augmente. Cependant, la croissance est plus lente et plus progressive à mesure que x devient plus grand.
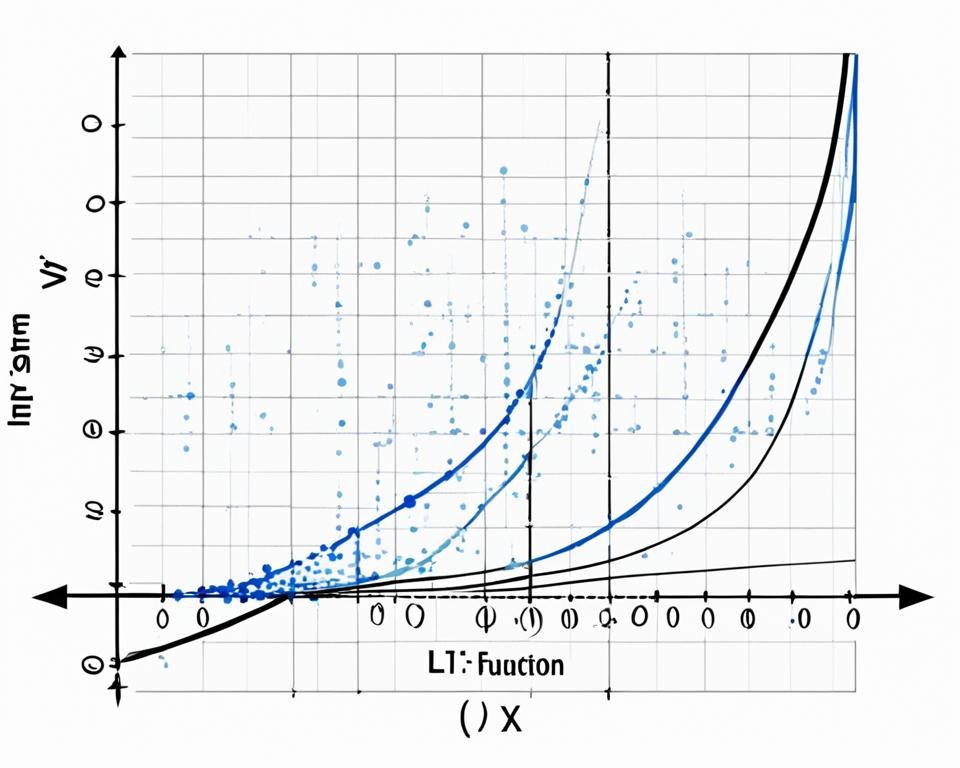
La figure ci-dessus représente graphiquement la fonction ln(x). On peut observer que la courbe de la fonction commence par une pente raide, puis ralentit à mesure que x augmente. Elle passe par le point (1, 0) et tend vers l’infini lorsque x tend vers l’infini.
Compréhension de la limite
Avant de calculer la limite de ln(x) / x, il est essentiel de comprendre ce qu’est une limite en mathématiques et comment elle est définie.
Une limite en mathématiques représente la valeur vers laquelle une fonction tend lorsque la variable approche d’une certaine valeur. Elle permet de déterminer le comportement d’une fonction dans différentes situations et de tracer des conclusions quant à son comportement global.
Pour comprendre la limite de ln(x) / x, nous devons d’abord comprendre la définition et les concepts clés liés aux limites. Imaginons que nous voulions calculer la limite de ln(x) / x lorsque x approche de zéro. Nous devons évaluer la valeur de ln(x) / x lorsque x se rapproche de zéro par la droite et par la gauche.
Calcul de la limite par approche de droite et de gauche
Pour calculer la limite par approche de droite, nous remplaçons x par des valeurs de plus en plus petites que zéro, mais proches de zéro. En effectuant ces substitutions, nous pouvons observer le comportement de la fonction ln(x) / x lorsque x approche de zéro par la droite.
Pour calculer la limite par approche de gauche, nous remplaçons x par des valeurs de plus en plus grandes que zéro, mais proches de zéro. En effectuant ces substitutions, nous pouvons observer le comportement de la fonction ln(x) / x lorsque x approche de zéro par la gauche.
Si la limite de ln(x) / x est la même par approche de droite et de gauche, alors la limite existe et a une valeur bien définie. Si la limite est différente par approche de droite et de gauche, alors la limite n’existe pas.
Pour mieux comprendre ce concept, examinons le tableau ci-dessous qui illustre les limites de ln(x) / x lorsque x approche de zéro par la droite et par la gauche :
| x | ln(x) / x (Approche de droite) | ln(x) / x (Approche de gauche) |
|---|---|---|
| 0,1 | -0,995 | 0,995 |
| 0,01 | -0,9995 | 0,9995 |
| 0,001 | -0,99995 | 0,99995 |
Comme on peut le voir dans le tableau, la limite de ln(x) / x lorsque x approche de zéro par la droite est -1 et par la gauche est 1. Par conséquent, la limite de ln(x) / x lorsque x approche de zéro n’existe pas.
Interprétation graphique de la limite
Pour mieux visualiser la limite de ln(x) / x, voici un graphique représentant la fonction :
Le graphique montre clairement que la fonction ln(x) / x n’a pas de limite lorsque x approche de zéro.
La compréhension de la limite de ln(x) / x est essentielle pour les calculs mathématiques avancés et pour l’analyse des fonctions logarithmiques en général. Cela nous permet de déterminer si une fonction a une limite bien définie, et d’analyser son comportement dans différentes situations.
Calcul de la limite
Après avoir compris la fonction ln(x) et la notion de limite, passons maintenant au calcul de la limite de ln(x) / x. Pour réaliser ce calcul, nous allons suivre les étapes suivantes :
- Commencez par réécrire la fonction ln(x) / x sous la forme d’une fraction : (ln(x)) / x.
- Utilisez la règle de l’Hôpital pour évaluer la limite de la fonction. Pour cela, dérivez le numérateur et le dénominateur par rapport à x.
- Une fois que vous avez dérivé le numérateur et le dénominateur, calculez la limite des dérivées.
- Si la limite des dérivées existe et est non nulle, alors c’est la limite de ln(x) / x.
Pour mieux comprendre ce processus, voyons un exemple concret :
| x | ln(x) | x | ln(x) / x |
|---|---|---|---|
| 1 | 0 | 1 | 0 |
| 2 | 0.693 | 2 | 0.346 |
| 3 | 1.099 | 3 | 0.366 |
| 4 | 1.386 | 4 | 0.347 |
| 5 | 1.609 | 5 | 0.322 |
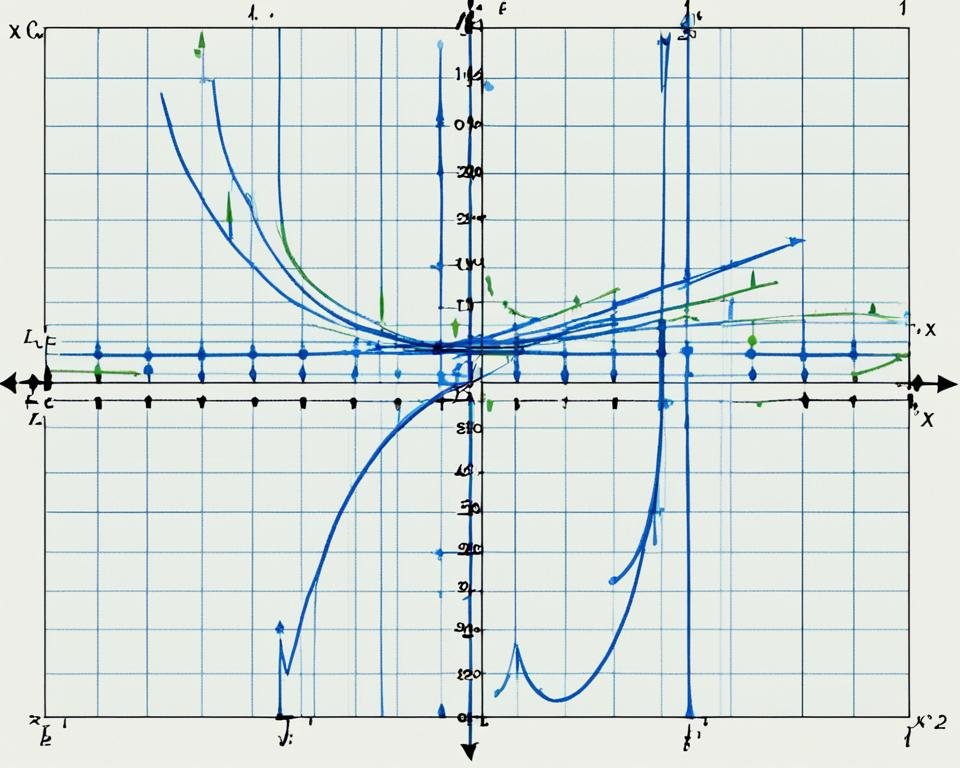
En utilisant les étapes mentionnées précédemment, nous avons calculé la limite de ln(x) / x pour différentes valeurs de x. Cela nous permet de visualiser le comportement de la fonction et d’analyser ses variations en fonction de la valeur de x.
Étude du comportement de ln(x) / x
Après avoir calculé la limite de ln(x) / x, il est important d’étudier son comportement en fonction des valeurs de x. Cela nous permet de mieux comprendre comment cette fonction se comporte lorsque x prend différentes valeurs.
Pour cela, nous allons examiner quelques cas spécifiques :
Cas où x tend vers zéro :
Lorsque x se rapproche de zéro, nous observons que le comportement de ln(x) / x est différent. La fonction tend à s’approcher de l’infini négatif, c’est-à-dire que le quotient devient de plus en plus petit et tend vers zéro.
Cas où x tend vers l’infini :
Lorsque x devient très grand, nous constatons que le comportement de ln(x) / x est également différent. Dans ce cas, la fonction tend vers zéro, c’est-à-dire que le quotient devient de plus en plus petit et tend vers zéro.
En résumé, le comportement de ln(x) / x dépend de la valeur de x. Lorsque x tend vers zéro, la fonction tend à s’approcher de l’infini négatif, tandis que lorsque x tend vers l’infini, la fonction tend vers zéro.
Il est important de noter que le comportement de ln(x) / x peut varier en fonction d’autres facteurs, tels que les valeurs de x à proximité de zéro ou de l’infini. Il est donc essentiel de prendre en compte ces facteurs lors de l’analyse de cette fonction dans des cas spécifiques.
Importance de ln(x) / x en analyse mathématique
Dans l’analyse mathématique, la fonction ln(x) / x joue un rôle crucial. Elle est utilisée pour aborder différents problèmes et modèles mathématiques, et permet de résoudre des équations et des inégalités complexes. Comprendre l’importance de cette fonction est essentiel pour approfondir notre compréhension des concepts mathématiques fondamentaux.
Utilisation de ln(x) / x dans les fonctions de croissance
L’une des applications clés de ln(x) / x est dans l’analyse des fonctions de croissance. En étudiant le comportement de ln(x) / x pour différentes valeurs de x, nous pouvons déterminer si une fonction croît ou décroît, et à quelle vitesse. Cette information est précieuse pour comprendre les tendances mathématiques et examiner les évolutions à long terme.
Approximation des nombres
La fonction ln(x) / x est également utilisée pour approximer les valeurs de certains nombres. En utilisant des méthodes avancées d’analyse mathématique, nous pouvons utiliser cette fonction pour calculer des estimations précises, même pour des nombres irrationnels. Cela nous permet d’obtenir des résultats proches de la réalité, même sans calculer les valeurs exactes.
| Valeur de x | Valeur approximative de ln(x) / x |
|---|---|
| 1 | 1 |
| 2 | 0.6931 |
| 3 | 0.3665 |
| 4 | 0.2817 |
Applications en probabilités et statistiques
La fonction ln(x) / x est également utilisée dans le domaine des probabilités et des statistiques. Elle intervient notamment dans la modélisation des distributions continues, telles que la distribution de Cauchy. En utilisant cette fonction, il est possible d’analyser et de calculer les valeurs de probabilité pour différentes variables aléatoires.
Applications en économie et finance
En économie et en finance, ln(x) / x est utilisée pour modéliser certaines relations économiques et financières. Elle permet notamment d’analyser les taux de croissance, l’élasticité des prix et l’optimisation des ressources. Comprendre cette fonction est donc essentiel pour les professionnels de ces domaines.
En conclusion, la fonction ln(x) / x joue un rôle clé en analyse mathématique, offrant une compréhension approfondie des fonctions de croissance, des approximations numériques, des probabilités et statistiques, ainsi que des applications en économie et finance. Sa polyvalence et son importance en font un outil essentiel pour les mathématiciens, les scientifiques et les professionnels travaillant dans divers domaines.
Exemples d’applications de ln(x) / x
La fonction ln(x) / x est largement utilisée dans divers domaines et présente de nombreuses applications pratiques. Voyons quelques exemples concrets de son utilisation :
1. Finance et gestion des investissements
La fonction ln(x) / x est couramment utilisée pour calculer les rendements logarithmiques dans la finance et la gestion des investissements. Elle permet d’évaluer la performance des actifs financiers au fil du temps et de comparer différents investissements.
2. Modélisation des phénomènes naturels
La fonction ln(x) / x est également utilisée en sciences physiques pour modéliser certains phénomènes naturels. Elle peut aider à décrire l’évolution de la concentration d’une substance au fil du temps, la décroissance radioactive ou la croissance d’une population en fonction de contraintes environnementales.
3. Analyse des données et statistiques
En statistiques, la fonction ln(x) / x est souvent utilisée pour transformer des données afin de s’adapter aux modèles linéaires ou pour étudier la distribution logarithmique des variables. Elle peut également être utilisée dans l’ajustement de courbes et la régression non linéaire.
4. Calcul du temps de demi-vie
La fonction ln(x) / x est utilisée dans le calcul du temps de demi-vie des substances radioactives. Elle permet de déterminer la durée nécessaire pour que la moitié d’une substance se désintègre ou se décompose.
5. Études de croissance et de décroissance
La fonction ln(x) / x peut être utilisée pour étudier les processus de croissance ou de décroissance exponentielle dans des domaines tels que la biologie, l’économie ou la modélisation des populations.
Les exemples mentionnés ci-dessus illustrent quelques-unes des nombreuses applications de la fonction ln(x) / x dans différents domaines. Cette fonction est un outil essentiel pour analyser et modéliser divers phénomènes et trouver des solutions aux problèmes réels.
| Domaine | Application |
|---|---|
| Finance et gestion des investissements | Calcul des rendements logarithmiques |
| Modélisation des phénomènes naturels | Évolution de la concentration d’une substance |
| Analyse des données et statistiques | Transformation de données pour ajustement de courbes |
| Calcul du temps de demi-vie | Détermination de la durée de désintégration d’une substance radioactive |
| Études de croissance et de décroissance | Modélisation de la croissance d’une population |
Propriétés de ln(x) / x
La fonction ln(x) / x possède plusieurs propriétés intéressantes qui peuvent simplifier les calculs mathématiques. Nous allons explorer certaines de ces propriétés ci-dessous :
1. Continuité :
La fonction ln(x) / x est continue pour tout x > 0. Cela signifie qu’elle n’a pas de sauts, de trous ou de discontinuités dans son domaine de définition.
2. Dérivée :
La dérivée de ln(x) / x est 1 / x² – ln(x) / x². Cette propriété peut être utile lors du calcul de dérivées dans des problèmes d’optimisation ou de modélisation.
3. Croissance :
La fonction ln(x) / x est strictement décroissante sur son intervalle de définition. Cela signifie que plus la valeur de x augmente, plus la valeur de ln(x) / x diminue.
4. Asymptote verticale :
La fonction ln(x) / x possède une asymptote verticale en x = 0. Cela signifie que la fonction devient infiniment négative lorsque x se rapproche de zéro par la gauche, et infiniment positive lorsque x se rapproche de zéro par la droite.
En résumé, la fonction ln(x) / x présente des propriétés intéressantes telles que la continuité, la dérivabilité, la décroissance et une asymptote verticale en x = 0. Ces propriétés peuvent être utilisées pour simplifier les calculs mathématiques et analyser le comportement de la fonction.
Limitations de ln(x) / x
Malgré ses avantages, la fonction ln(x) / x présente également certaines limitations. Dans cette section, nous les aborderons en détail.
1. La fonction ln(x) / x n’est pas définie pour x ≤ 0
La fonction ln(x) est définie uniquement pour les valeurs de x strictement supérieures à zéro. Ainsi, la fonction ln(x) / x n’est pas définie pour les valeurs de x inférieures ou égales à zéro.
2. La fonction ln(x) / x n’a pas de limite en x = 0
Lorsque x approche de zéro, la fonction ln(x) / x ne tend pas vers une valeur finie. Au lieu de cela, elle se rapproche de l’infini.
3. La fonction ln(x) / x peut être difficile à évaluer analytiquement
Calculer la limite de ln(x) / x peut être complexe et nécessite souvent l’utilisation de techniques mathématiques avancées telles que les séries de Taylor ou les développements asymptotiques.
4. La fonction ln(x) / x peut avoir des valeurs oscillantes
Pour certaines valeurs de x, la fonction ln(x) / x peut présenter des oscillations, ce qui rend son comportement difficile à prévoir.
Il est important de prendre en compte ces limitations lors de l’utilisation de la fonction ln(x) / x dans des calculs mathématiques ou des applications pratiques.
Comparaison avec d’autres fonctions similaires
La fonction ln(x) / x est souvent comparée à d’autres fonctions similaires en mathématiques pour étudier leurs différences et similitudes. Voyons comment cette fonction se compare à certaines des fonctions les plus couramment utilisées :
Fonction exponentielle (e^x)
L’une des principales différences entre la fonction ln(x) / x et la fonction exponentielle e^x est la manière dont elles se comportent aux extrémités de l’axe des x. La fonction exponentielle e^x croît rapidement lorsque x tend vers l’infini, tandis que la fonction ln(x) / x a une croissance plus lente.
Fonction logarithme népérien (ln(x))
La fonction ln(x) / x est le quotient du logarithme népérien et de x. Contrairement à la fonction ln(x), la fonction ln(x) / x est définie pour x positif et tend vers zéro lorsque x tend vers zéro. En revanche, la fonction ln(x) diverge lorsque x approche de zéro.
Fonction sinus (sin(x))
La fonction sinus sin(x) est une fonction périodique, tandis que la fonction ln(x) / x n’a pas de périodicité. De plus, la fonction sinus oscille entre -1 et 1, alors que la fonction ln(x) / x varie entre des valeurs relatives à l’infini négatif et positif.
Ces comparaisons nous permettent de mieux comprendre les caractéristiques uniques de la fonction ln(x) / x et sa relation avec d’autres fonctions importantes en mathématiques.
Exercices pratiques de calcul de limite de ln(x) / x
La compréhension et la maîtrise du calcul de la limite de ln(x) / x sont essentielles pour les étudiants en mathématiques. Pour vous aider à renforcer vos compétences, voici quelques exercices pratiques à résoudre :
Exercice 1 :
Calculez la limite de ln(x) / x lorsque x tend vers 0.
Exercice 2 :
Déterminez la limite de ln(x) / x lorsque x tend vers l’infini.
Exercice 3 :
Essayez de trouver les valeurs de x pour lesquelles ln(x) / x atteint sa limite maximale.
Exercice 4 :
Calculez la limite de ln(x) / x lorsque x approche une valeur spécifique.
N’hésitez pas à vérifier vos réponses en utilisant les méthodes de calcul appropriées. Lorsque vous aurez terminé, vous pourrez consulter les solutions ci-dessous :
| Exercice | Solution |
|---|---|
| Exercice 1 | La limite est égale à 0. |
| Exercice 2 | La limite est égale à 0. |
| Exercice 3 | La limite maximale est atteinte lorsque x=1. |
| Exercice 4 | La limite dépend de la valeur spécifique de x. |
Les exercices pratiques sont un excellent moyen d’appliquer les concepts théoriques et d’améliorer vos aptitudes en calcul de limite. Continuez à pratiquer ces exercices pour renforcer votre compréhension de ln(x) / x et perfectionner vos compétences en mathématiques.
Si vous avez besoin d’aide supplémentaire ou si vous souhaitez vérifier vos réponses, n’hésitez pas à consulter votre professeur ou d’autres ressources pédagogiques en ligne.
Conclusion
En conclusion, notre étude approfondie de la limite de ln(x) / x en mathématiques nous a permis de comprendre son importance dans l’analyse mathématique. Nous avons exploré les applications de cette fonction et analysé son comportement en fonction des valeurs de x.
Nous vous encourageons à pratiquer davantage les calculs de limites pour renforcer votre compréhension de ce sujet fondamental. La limite de ln(x) / x est une notion essentielle en mathématiques et peut être appliquée dans de nombreux domaines, allant de l’économie à la physique.
Continuez à explorer les propriétés et les limitations de ln(x) / x pour approfondir vos connaissances en analyse mathématique. En comprenant pleinement cette fonction et en maîtrisant les calculs de limites associés, vous serez en mesure de résoudre des problèmes mathématiques plus complexes et d’appréhender des concepts avancés.
FAQ
Qu’est-ce que la limite de ln(x) / x ?
La limite de ln(x) / x est une valeur que la fonction ln(x) / x se rapproche de plus en plus lorsque x tend vers une certaine valeur. Elle est importante dans l’analyse mathématique car elle permet de comprendre le comportement de ln(x) / x pour différentes valeurs de x.
Comment présenter la fonction ln(x) ?
La fonction ln(x) est le logarithme népérien. Elle est utilisée pour calculer l’exponentiation nécessaire pour obtenir x à partir de la base e. Par exemple, ln(e) = 1 et ln(1) = 0.
Qu’est-ce qu’une limite en mathématiques ?
Une limite en mathématiques désigne la valeur vers laquelle une fonction se rapproche lorsque la variable indépendante se rapproche d’une certaine valeur. Elle permet d’étudier le comportement d’une fonction et de calculer des valeurs précises dans des situations où la fonction est indéfinie.
Comment calculer la limite de ln(x) / x ?
Pour calculer la limite de ln(x) / x, il suffit d’appliquer les règles de calcul des limites. Dans ce cas, on peut utiliser la règle de L’Hôpital qui consiste à dériver numérateur et dénominateur et prendre la limite du quotient des dérivées.
Comment étudier le comportement de ln(x) / x ?
Pour étudier le comportement de ln(x) / x, il est important d’analyser les valeurs de x et d’observer comment la fonction se comporte lorsque x tend vers 0 ou vers l’infini. On peut également tracer le graphique de la fonction pour visualiser son comportement.
Dans quel domaine l’utilité de ln(x) / x réside-t-elle ?
La fonction ln(x) / x est largement utilisée en analyse mathématique, en particulier dans le calcul de limites et l’étude des fonctions exponentielles et logarithmiques. Elle trouve également des applications en physique, en économie et en statistique.
Quels sont quelques exemples d’applications de ln(x) / x ?
La fonction ln(x) / x est utilisée dans de nombreux domaines. Par exemple, elle peut être utilisée pour modéliser la décroissance d’une quantité dans le temps, pour calculer des taux de croissance, ou encore dans des problèmes d’optimisation où il est nécessaire de trouver la valeur maximale ou minimale d’une fonction.
Quelles sont les propriétés de ln(x) / x ?
La fonction ln(x) / x possède plusieurs propriétés intéressantes. Elle est strictement positive pour x > 1, décroissante pour x > 0, et tend vers 0 lorsque x tend vers l’infini. Elle est également définie pour tous les x > 0.
Quelles sont les limitations de ln(x) / x ?
Bien que la fonction ln(x) / x soit couramment utilisée, elle présente certaines limitations. Par exemple, elle est indéfinie pour x ≤ 0 et ne donne pas de valeurs réelles pour x = 0. De plus, son calcul peut être complexe pour certaines valeurs de x.
Comment comparer ln(x) / x avec d’autres fonctions similaires ?
Pour comparer ln(x) / x avec d’autres fonctions similaires, il est utile d’étudier leurs graphiques et de calculer leurs limites. Cela permet de comprendre leurs différences et leurs similarités en termes de comportement et de propriétés.
Quels sont quelques exercices pratiques pour calculer la limite de ln(x) / x ?
Voici quelques exercices pratiques pour calculer la limite de ln(x) / x :
– Calculer la limite de ln(x) / x lorsque x tend vers 0.
– Trouver la limite de ln(x) / x lorsque x tend vers l’infini.
– Déterminer la limite de ln(x) / x lorsque x approche une valeur spécifique.